
(It should be noted that although the output value of 11 repeats, only the input value cannot) We can also see this is a function by the list of ordered pairs since none of the x-values repeat: (*1,1), (1,1), (7,49), and (0.5,0.25) because each input maps to exactly one output. The illustration shows that every value of the domain has a green arrow pointing to the corresponding value of the range. The green arrows show how each member of the domain is mapped to a particular value in the range. The oval on the left represents the domain of the function f, and the oval on the right represents the range. The rule for a function is that every input will yield exactly one output. Functions are relationships that take inputs in one domain and output values in another. As shown in the illustration below, the range of the function is the set of values it outputs, and these values are indicated by the right-hand oval. A value is provided by the function, f(x), for every member of the domain. This domain is represented by the oval on the left in the image below. What Is the Domain and Range of a Function?Īn input domain, or domain of a function, is a set of values that a function can be used to evaluate.
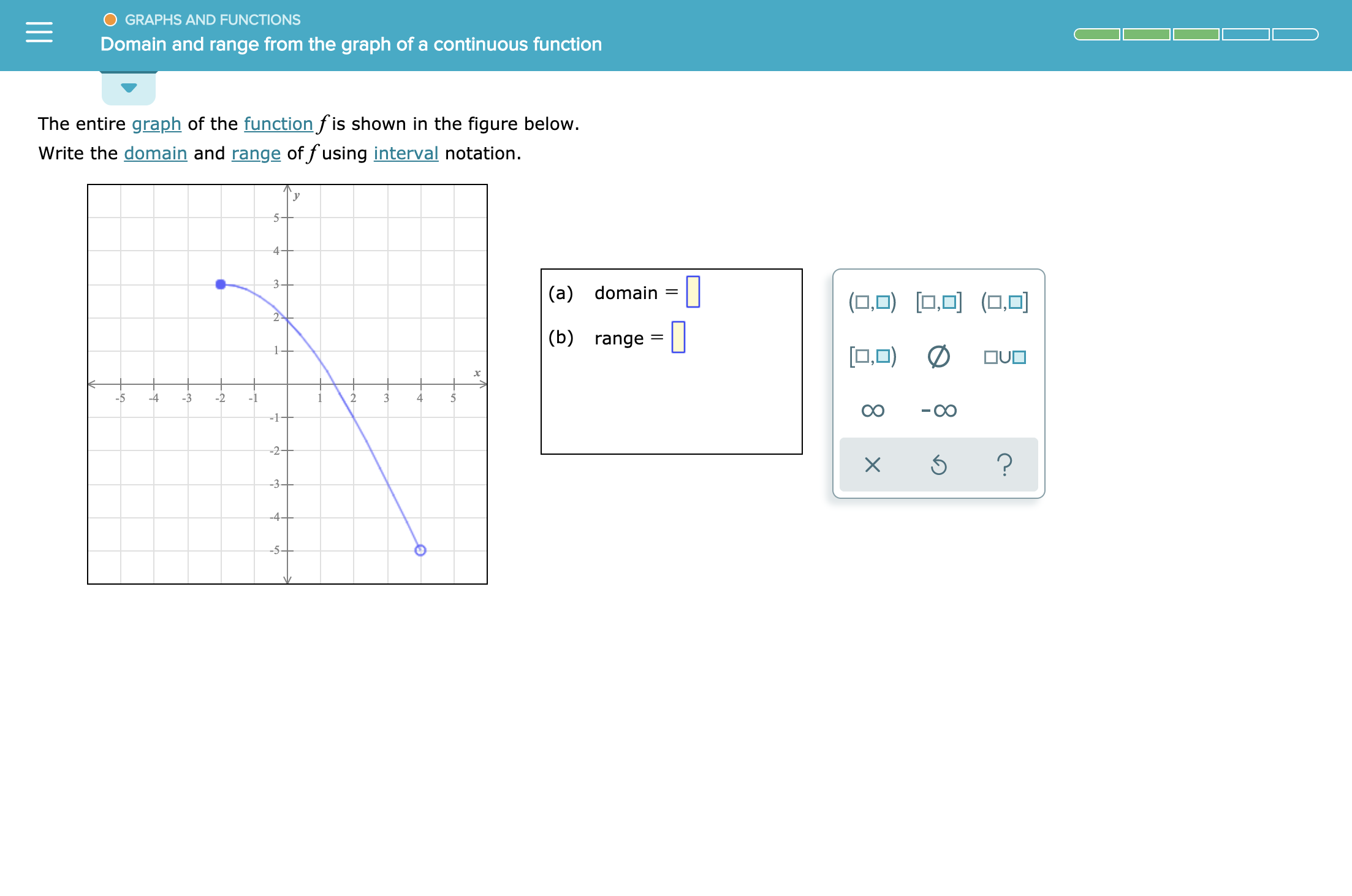

The domain and range calculator can be used by following the steps below: For a circle, you can draw a vertical line that intersects at two points, and hence it is not a function.How to Use the Domain and Range Calculator? A graph is that of a function if and only if no vertical line intersects the graph at more than one point. The test states that a graph is of a function if no vertical line intersects the graph in more than one point.Īns: The vertical line test can be used to find whether a graph is a function or not. How do you know if a graph is a function?Īns: To understand whether a graph is a function, the vertical line test is used. The graph of a function \(f\) is the graph of the equation \(y = f\left( x \right).\) That is, it is the set of all points \(\left( \right).\) So, the function rule can be identified from the points on a graph as each point has the values of dependent and independent variables that are related to each other via that function rule, thus identifying the function. How do you find the function of a graph?Īns: Functions are defined with a function rule – the rule with which the dependent and the independent variables are related. For example, for the function \(f\left( x \right) = 3x – 5\) the rule is to multiply the variable by \(3\) and subtract \(5.\) Frequently Asked Questionsīelow are some Frequently Asked Questions from Graphs of Functions.Īns: When a function is defined from a set \(A\) to set \(B,\) the image of an independent variable is related to the independent variable with some set rules. Later the article explains a few characteristics of a function visible in their graphs and concludes with a few solved examples to strengthen the concepts discussed. The article also discusses the definition and the graphs of various functions such as constant, linear, identity, modulus, greatest integer function, smallest integer function, signum function, exponential, logarithmic, rational and polynomial functions.įurther, it explores the vertical line test, which helps you classify a relation into a function. The article helps you understand the basics of functions and the ways to represent those using graphs.


 0 kommentar(er)
0 kommentar(er)
